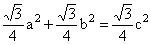Una sucesión es un conjunto ordenado de numeros asociados a un conjunto de índices (1,2,3,4,5,6.......)
Por ejemplo la sucesión de los números pares : a1 = 2, a2 = 4, a3 = 6, a4 = 8, a5 =10, a6 =1 2,......., an = 2·n (el primer par es el dos, el segundo el 4, el tercero el 6, ... el n-simo numero par es 2·n)
Este artículo trata sobre una sucesión particular, llamada Sucesión de Fibonacci.
Su definición es muy simple, pero tiene una serie de implicancias en la naturaleza, las artes y en múltiples ámbitos.
Se define de la siguiente forma
a1 = 1 ; a2 = 1 ; a3 = a1 + a2 = 1 + 1 = 2 ; a4 = a2 + a3 = 1 + 2 = 3 ; ..... an = an-2 + an-1
(Una vez definidos los dos primeros términos, cada término siguiente es igual a la suma de los dos anteriores)
Así la sucesión de Fibonacci será 1, 1, 2, 3 ,5, 8, 13, 21, 34, 55, 89, 144,......
EJEMPLOS DE APLICACIÓN
En un patio cerrado, se coloca una pareja de conejos para ver cuántos descendientes produce en el curso de un año, y se supone que cada mes a partir del segundo mes de su vida, cada pareja de conejos da origen a una nueva. Como la primera pareja de conejos tiene descendencia en el primer mes, dobla el número y, en este mes, se tienen dos parejas. De éstas, una pareja, la primera, también tiene descendencia en el mes siguiente, de manera que en el segundo mes hay tres parejas. De ésas, dos parejas tienen descendencia en el mes siguiente, de modo que en el tercer mes han nacido dos parejas adicionales de conejos, y el número total de parejas de conejos llega a cinco. En dicho mes tres de estas cinco parejas tienen hijos y, en el cuarto, el número de parejas llega a 8. Cinco de estas parejas producen otras cinco parejas, las cuales, junto con las 8 parejas ya existentes, hacen 13 parejas en el quinto mes. Cinco de estas parejas no tienen hijos en este mes en este mes, mientras que las restantes ocho parejas tienen descendencia, de modo que en el sexto mes se tienen 21 parejas. Simando a éstas las 13 parejas que nacen en el séptimo mes, se obtiene un total de 34 parejas. Sumando a éstas las las 21 parejas que nacen en el octavo mes, el total es de 55 parejas. Sumando a éstas las 34 parejas que nacen en el noveno mes, se obtienen 89 parejas. Agregando a éstas las 55 parejas que nacen en el décimo mes, se tiene un total de 144 parejas. Agregando a éstas las 89 parejas que nacen en el undécimo mes, se llega a un total de 233 parejas.
Finalmente, sumando a éstas 144 parejas que nacen en el último mes, se obtienen un total de 377 parejas. Este es el número de parejas producidas por la primera pareja en el lugar dado, al término de un año. Al examinar la tabla anterior, el lector puede ver cómo se llega a este resultado; a saber: se suma el primer número al segundo, o sea, 1 a 2; el segundo al tercero; el tercero al cuarto, el cuarto al quinto; y así sucesivamente, hasta que se suman el décimo y el undécimo números 144 y 233; así se obtiene el número total de parejas de los conejos en cuestión, es decir, 377."
Parejas:
Inicio del Año 1
primer mes 2
segundo mes 3
tercer mes 5
cuarto mes 8
quinto mes 13
sexto mes 21
séptimo mes 34
octavo mes 55
noveno mes 89
décimo mes 144
undécimo mes 233
duodécimo mes 377
Otra Aplicación:
Si cuentas las escamas de una piña, observarás sorprendido que aparecen en espiral alrededor del vértice en número igual a dos términos consecutivos de la sucesión de Fibonacci
Lo mismo ocurre con las piñas de girasol; forman una red de espirales, unas van en sentido de las agujas del reloj y otras en el contrario, pero siempre las cantidades de unas y de otras son los términos consecutivos de la sucesión de Fibonacci.
La espiral tambien surge de los números de Fibonacci
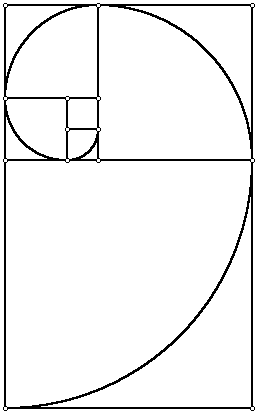
Si el primer cuadrado tiene lado 1, junto a él se ha dibujado un nuevo cuadrado de lado 1, trazando un arco de 90º. Luego se ha dibujado un nuevo cuadrado tomando como lado el total del lado de la figura anterior, s decir la medida es 2, se vuelve a trazar el arco de 90º. Luego se vuelve a dibujar un cuadrado apoyado en el lado de la figura, teniendo éste lado igual a 3. Al continuar el proceso, las medidas de los lados serán 1,1,3,5,8,13 ... es decir, los numeros de la Sucesión de Fibonacci.
Un ejercicio interesante es escribir los números de la sucesión en Base 2...
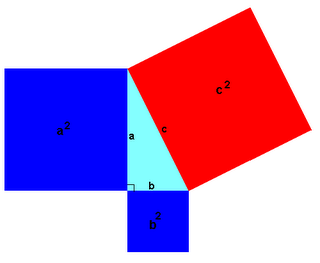
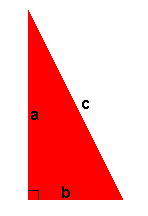
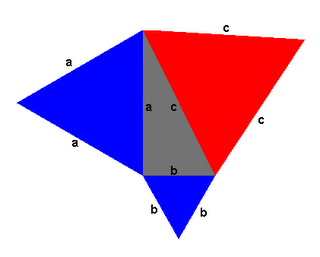
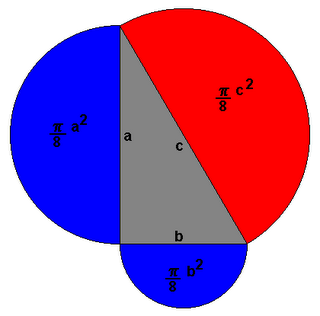
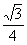 para obtener En realidad, puede extenderse la versión geometrica del teorema de pitágoras a cualquier polígono regular de n lados, pues el área de un poligono regular n lados de medida x esta dada por la expresión
para obtener En realidad, puede extenderse la versión geometrica del teorema de pitágoras a cualquier polígono regular de n lados, pues el área de un poligono regular n lados de medida x esta dada por la expresión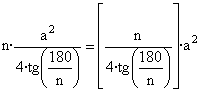
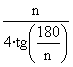 sólo depende del número de lados del polígono.
sólo depende del número de lados del polígono.